Finding the Stationary Points for the Given Function.

1.1 Module introduction

If the function is twice differentiable, the stationary points that are not turning points are horizontal inflection points. The first two options are collectively known as " local extrema ".

• About the author;
• Applying differential calculus.
• Evangelismo e Testemunho: a sua autêntica missão de apresentar Jesus às pessoas (Portuguese Edition)!
• How do I find where the stationary points of a function are??
• The Therapists Notebook for Integrating Spirituality in Counseling I: Homework, Handouts, and Activities for Use in Psychotherapy: v. 1 (Haworth Practical Practice in Mental Health)!

Similarly a point that is either a global or absolute maximum or a global or absolute minimum is called a global or absolute extremum. The last two options—stationary points that are not local extremum—are known as saddle points.

Determining the position and nature of stationary points aids in curve sketching of differentiable functions. The specific nature of a stationary point at x can in some cases be determined by examining the second derivative f'' x:. A more straightforward way of determining the nature of a stationary point is by examining the function values between the stationary points if the function is defined and continuous between them.

More generally, the stationary points of a real valued function f: The reason is that the sign of f' x changes from negative to positive. But this is not a stationary point, rather it is a point of inflection. This is because the concavity changes from concave downwards to concave upwards and the sign of f' x does not change; it stays positive.

This is both a stationary point and a point of inflection. From Wikipedia, the free encyclopedia. This article is about stationary points or critical points of a real-valued function of one real variable. For the general notion, see Critical point mathematics. This article includes a list of references , but its sources remain unclear because it has insufficient inline citations. Therefore the gradient at either side of the stationary point needs to be looked at alternatively, we can use the second derivative. At maximum points, the gradient is positive just before the maximum, it is zero at the maximum and it is negative just after the maximum.

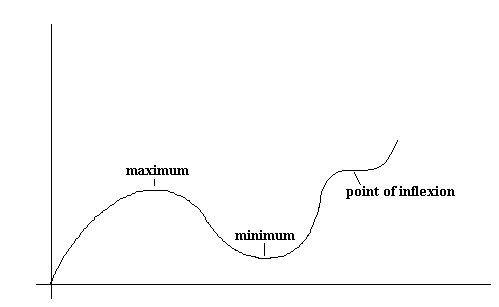
At minimum points, the gradient is negative, zero then positive. Finally at points of inflexion, the gradient can be positive, zero, positive or negative, zero, negative. This is illustrated here:.

This method of finding maxima and minima is very useful and can be used to find the maximum and minimum values of all sorts of things. Find the least area of metal required to make a closed cylindrical container from thin sheet metal in order that it might have a capacity of p cm 3. So we have an expression for the surface area. You should then check that this is indeed a minimum using the technique above. Therefore the minimum amount of metal required is p cm 2.

Skip to main content. Increasing and Decreasing Functions An increasing function is a function where: We can use differentiation to determine if a function is increasing or decreasing: Stationary Points Stationary points are points on a graph where the gradient is zero.

• 30 Ways To Lower Blood Pressure Naturally - A Step By Step Plan To Reduce Blood Pressure Quickly;
• Partial Differentiation: Stationary Points.
• Medicare’s Birth in Saskatchewan: 50th anniversary of a people’s victory.
• BBC Bitesize - Higher Maths - Applying differential calculus - Revision 1!
• Campaign Pictures of the War in South Africa (1899-1900) Letters from the Front?
• Ultra-Wideband and 60 GHz Communications for Biomedical Applications;
• Stationary Points.

The three are illustrated here: Maximum, Minimum or Point of Inflection?