The relief of the host face of a crystal plays an important role in the processes of adsorption i. From the point of view of the adsorption phenomenon the smoothness of a crystal face is a relative notion; it depends both on the structure of the face and on the size of the adsorbate atom ion. For instance, for the adsorption of a cesium atom with its large radius, the face of tungsten Fig.
However, the same plane may be regarded as a rough one for the adsorption of lithium or copper atoms whose atomic radius is small in comparison with the atomic or even ionic radius of tungsten.
Navigation menu
Usually, low-index faces are thought to be smooth and the ones with high Miller indices are regarded as rough. Although conventional, such a classification is, of course, arbitrary. Structure of the surface is specified by taking the unperturbed net of the substrate plane with its known structure and Miller indices as the reference lattice. It is easy to see that the surface area of unit cell of the lattice bl, b2 is equal to the product of the determinant value of the matrix M, det M, and the surface area of unit cell of the lattice al, a2.
The value of det M allows to classify the resulting structures in the following way: In the case when the angles between the base translation vectors of the lattice bl, b2 and al,a2 are equal, a notation proposed by Elisabeth Wood is commonly used. A letter p may precede the parenthesis when the unit cell of the new surface lattice is primitive or a letter c, when the unit cell is centered. Examples of two-dimensional surface structures denoted according to the Wood nomenclature: Illustrations of some surface structures are given in Fig.
However, in general the term surface means a few of last atomic layers of the solid, whose geometrical or electron structure has been disturbed by breaking of the translational symmetry of the crystal in the direction normal to the surface. Surfaces can be divided into the idealized perfect ones, which do not exhibit any lattice defects vacancies, impurities or intrusions, stacking faults, etc. Usually a perfect surface is thought of as a lattice plane revealed by the ideal cleavage of single crystal into two parts, parallel to the crystallographic plane, without changing atomic configuration in either resulting parts.
In practice, the use of single crystals enables to eliminate point defects but total elimination of dislocations is not possible.
Metal Surface Electron Physics
In order to avoid impurities the measurement should be carried out under ultrahigh vacuum conditions i. Under the vacuum conditions of 10 -9 Torr this time extends to one hour. The knowledge and understanding of the properties of perfect surfaces and their link with the properties of the bulk crystal is of great importance in understanding of the properties of real surfaces. In general, under usual experimental conditions, such perfect surfaces cannot be obtained.
In some cases, however, a carefully prepared surface may be considered as a perfect one. The density of dislocation in metals, which typically amounts to l0 s per cm 2, can be reduced by one or two orders of magnitude. A comparison of the two latter numbers demonstrates that any information about surface atoms must 1The unit 1 Torr - 1 mm Hg - Schematic view of a surface atom and its nearest atomic surrounding. Structure of a surface plane of the perfect single crystal should coincide with t h a t of the inner lattice planes parallel to the plane of interest.
However, any atom at the surface of a truncated crystal has quite a different spatial environment than atom in the bulk. The number of its neighbouring atoms is considerably less than t h a t of an interior atom Fig. Thus, the total energies of interaction are different for a surface atom and the one in the bulk. The interaction of an inner atom is characterized by a stronger binding than for a surface one. For the same structure, an atom lying in the plane has only 9 nearest neighbours whereas on the face the number is 8 and on the it has only 7 nearest neighbours.
Thus, thinking in terms of the bonds, on these faces there are three, four and five bonds less, with respect to bulk environment. The phenomenon leading to a rigid change of the distance between surface planes, without changing the two-dimensional unit cell is called surface relaxation of the lattice.
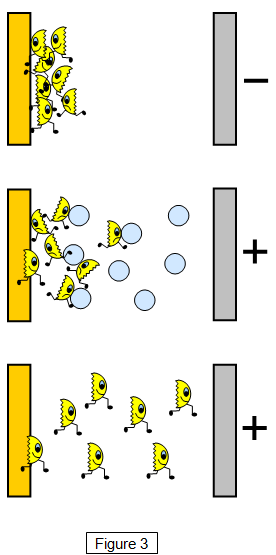
Also, segregation of one of the alloy-forming elements may occur on a surface of a single crystal of alloy. Moreover, owing to adsorption of foreign atoms onto a surface a new surface structure, quite different from that of the substrate, may be formed. The above surface processes are schematically illustrated in Fig.
In the case of metals we cannot speak about the orientational bonding. Schematic classification of surface processes which modify the structure of the surface lattice. Selected measured relaxations for low-index faces of several metals are collected in Table 2. From a comparison of numbers given in the table follows that majority of the low-index faces shows a contraction of the interplanar spacing. It can be seen as well that smaller relaxations are observed on close-packed faces such as the fcc and , bcc and hcp Relatively large changes in the interplanar spacings contractions are observed on the most open low-index faces of metals.
This concerns the face of the fcc structure and the or face of the bcc structure. This seems to indicate an increase of relaxation with decreasing density of packing in crystallographic planes or, in other words, with increasing roughness of the planes. Now, we may define surface roughness as the ratio of the area of surface plane to the area occupied in this plane by intersections of atoms of the radii equal to one half the bulk nearest-neighbour distance. The magnitude of relaxations for the six faces of an iron single crystal versus the roughness Sokolov et al.
Top-layer relaxation versus roughness at iron-crystal faces. Redrawn with permission from Sokolov et al.
- Quantitative Assessment of Securitisation Deals (SpringerBriefs in Finance).
- Metal Surface Electron Physics 0080426751;
- Als ich ein Kunstwerk war: Roman (German Edition).
- Havens Quest (Haven Series Book 1).
- Information Management and Technology: further advice and guidance on curriculum (Society and College of Radiographers Policy and Guidance)?
- Metal Surface Electron Physics (eBook);
- Hotel California!
A main role in this model is played by electrostatic forces exerted on the surface atoms. The force that is acting on a surface ion core equals the electrostatic force of the interaction with all the other ions and with the electronic charge density. In the case of simple metals we can assume that in a zeroth approximation the electronic density is uniformly spread out over the volume of the crystal and sharply cut off at its geometrical surface Fig. As can be seen from this figure, ions of the surface layer are located in asymmetric Wigner-Seitz cells.
The positive and negative charges in each cell must neutralize themselves mutually. Thus, an electrostatic force, oriented towards the bulk of metal, will be exerted on each surface ion along the direction of the electrostatic centre of gravity of each cell. Consequently, the ions dwelling the surface cells will be shifted towards the bulk and the interplanar distance between the first and the second ionic layers will be shortened.
This simple model leads to a good estimation of the largest contraction of the spacing for the roughest faces of the crystal. This is related to the fact that, the more asymmetric a cell is the greater is the force which acts on the ion to displace it towards the gravity centre of the cell. Complete calculations within the framework of the Finnis-Heine model should take into account the modification of the electronic density distribution, due to the displacement of the ions.
Thus, full selfconsistency in 3By simple metals we understand the s-p bonded metals where the d and f electrons do not play an important role. Asymmetric Wigner-Seitz cells at a surface. The Finnis-Heine model is not applicable to explain relaxations at noble or transition metals surfaces.
To account for the effect of localized d-electrons on the shortening of interplanar spacing at transition metal surfaces the first principles total energy calculations have to be performed Fu et al. More recent experimental data on the surface relaxation revealed the existence of damped-oscillatory multilayer relaxations. On rough faces, besides the oscillatory relaxation, also displacements of the surface atomic layer in the direction parallel to the surface are observed not necessarily accompanied by the change in the twodimensional lattice.
For instance, for the Fe face, the outer ionic layer is shifted relatively to the neighbouring one by 0. The active forces of the displacement tend to place the atoms in more symmetrical sites with respect to the position of atoms of the layer lying beneath, i. It is reasonable to expect that such sites correspond to the minimum of energy.
The measured magnitudes of the oscillatory surface relaxation are in quite a good agreement with theoretical predictions within the electrostatic model accounting for the three-dimensional screening response 2. Such calculations based on the total energy minimization, as well as the calculations within the effective-medium theory Jacobsen et al. Thus a surface ion in the topmost layer surrounded by lower than optimum electron density will be shifted inward. The more rough the plane is, the lower density surrounds ions and the larger displacement is required to reach the optimum density region.
The shortening of the topmost layer will cause an increase of the electron density around the second-layer atoms above the optimum value. As a consequence, to compensate for this, the ions of second layer shift outwards expanding the distance between the second and the third layer Stensgaard, An extension of the Finnis-Heine model, which enables to describe both the multilayer relaxation and the displacement of the outermost layer in parallel to the surface, was made by a semi-empirical electrostatic model of Jiang et al. Among the energy terms contributing to the total energy of the crystal it is mainly the electrostatic energy which is sensitive to the variation of the geometrical structure.
Thus looking for the minimum of the total energy to a first approximation, we may limit ourselves to the minimum of the electrostatic energy of metal.
Dividing the metal into electrically neutral layers Fig. Illustration of the method of summation over the surface cells. A denotes the area of the surface unit cell of the plane lattice. The energy E1 attains its minimum when the ionic lattice coincides with the centre of the layer. The summation in 2. Thus, the factor C appearing in 2. The value of the factor C can be adjusted for each metal to fit best to the experimental data.
At the values of Khd fixed by the geometrical structure of the bulk of metal, the structure of a relaxed surface is found 2. The model, by using the empirical parameter once adjusted for a given metal, demonstrates a good accordance with experiment for almost all the observed surface relaxations. Another crystallographic problem being the subject of intensive studies is surface reconstruction. Geometrical structure of a reconstructed surface plane differs from the bulk ones by arrangement of atoms which are displaced less or more from their equilibrium positions or even removed in part.
In other words, in a surface layer, a two-dimensional atomic lattice is formed which has different periodicity than the planes lying beneath, in the bulk. A similar type of structural transitions is observed also on the clean Mo Besides these clean-surface reconstructions, the adsorption-induced reconstructions are also observed. In this case the periodicity of the surface net may be determined either by the periodicity of adsorbate atoms only, or by the periodicity of the reconstructed substrate.
The adsorption of foreign atoms may also lead to the removal of already existing reconstructions on clean surface. It should be noted that the question why a crystal surface is subject to reconstruction or, in other words, why the reconstructed surfaces are energetically more favorable, can be answered only by the complete calculations of the surface electronic structure accounting for stresses existing on metals surface cf. This is manifested, among others, by an increased amplitude of thermal vibration of surface atoms. The experimental method of low energy eV electron diffraction LEED is particularly useful to investigate the vibration of surface atoms.
The LEED pattern which, in fact, is a representation of the reciprocal lattice of the surface structure can be realized only when the Laue condition for diffraction or the equivalent Bragg's condition is fulfilled. Let Rn be the vector of a plane Bravais lattice in the form of equation 1. The intensity of the diffraction beam diminishes with increasing temperature of the crystal. Simultaneously, the intensity of the diffusive background pattern is increased, which can be explained as being due to the atomic vibration which in turn implies the diffraction condition not to be fully satisfied.
Assuming that the atoms perform harmonic vibration, the intensity I, can be written as I T -- Ioe -2W, 2. Taking into account 2. As it is seen from 2. On the other hand, from the theory of lattice vibration within the framework of the harmonic approximation follows that the amplitude of vibration can be expressed by the force constants, C, proportionality constants of interatomic interactions. Let us notice that a surface atom possesses approximately half the number of nearest neighbours compared with an atom in the bulk. This means that surface force constant is softer than the one in the bulk.
Since the mean square displacement is related to the Debye temperature by equation 2. The examples of measured root-mean-square rms amplitudes of surface atoms and the corresponding surface Debye temperatures at the face of some fcc metals are given in Table 2. It follows from 2. The Debye temperature is dependent both on the atomic structure of the surface and on the ratio of area of the surface to the volume of the crystal. Consequently, upon measuring the Debye temperature of smaller and smaller crystals we should have observed the size effect, 4 i. The third column gives the ratio of rms amplitudes in the direction normal and parallel to the surface.
Data from Grudniewski and Mr6z Finally, it should be noted that although the harmonic approximation works well for the bulk Debye's temperatures, for the surface atoms the anharmonic effects may become of great importance leading to substantial changes in the values of In the above approximate analysis of surface vibration we have tacitly assumed that all observations are performed in the low temperature regime.
Although at elevated temperatures, the anharmonic effects should be taken into account, it occurs that our approximate analysis enables to draw certain conclusion regarding the phenomenon of melting of metals. It is known that, according to the Lindemann criterion Lindemann, a solid begins to melt when the amplitude of atomic vibrations is comparable with the nearest-neighbours distance R1N. In Debye's approximation when the Debye temperature is higher than the melting point of the crystal using 2. The melting point of sodium is K and its Debye temperature equals K.
Thus melting takes place when the root-mean-square amplitude of atomic vibration is roughly 0. Since the amplitude of vibration of surface atoms is higher than that of the ones in the bulk of crystal, from formulae 2. Surface melting at Pb The area of the surface peak of backscattered protons, expressed as the number of visible monolayers, as a function of temperature. Redrawn with permission from van der Veen and Frenken In the case of surface melting the atoms are removed from their lattice sites what results in a reduction of the short-range order and the formation of a liquid-like surface region.
The first demonstration of a reversible surface melting on Pb was provided by the Rutherford-backscattering experiment of Frenken and van der Veen As shown in Fig. Further increase of the temperature leads to a continuous increase in the thickness of disordered molten surface layer. Chapter 3 Thermodynamics of the surface of crystal 3. Thus, the first law of thermodynamics is formally expressed by U: If the process of transition from state 1 to state 2 is infinitesimal, what may be denoted symbolically as: Namely, in the case of the equal potentials on both ends of a conductor there is no current flow i.
When the free energy, F, of any homogeneous phase is regarded as a function of the independent variables T, V, N, the chemical potential ttj is the partial differential coefficient of F with respect to each Nj i. Mechanical equilibrium for the systems interacting mechanically 4 Pl -- P2, 3. Equilibrium of mass when the systems exchange mass, i. A sketch of the two adjacent phases: If two phases in the case of interest saturated vapor of metallic atoms, phase 'prime', and the solid metal, phase 'bis' are bounded by each other, an interface region exists between the phases which occupies the area A Fig.
The quantity a is called the surface energy. We will come back to these problems in Section 3. The problem of the crystal shape that emerges upon crystallization from the saturated vapor under conditions of thermodynamic equilibrium, has rather a long story and was attacked for the first time by Gibbs Then it was treated by P.
Curie and Wulff , and later by Landau A method of determination of the equilibrium form of crystal was proposed also by Stransky and Khaischev compare Mutaftschiev, Using in addition the known relations 3. The volume V' of such polyhedron can be expressed as the sum of the volumes of pyramids whose bases are the faces of the polyhedron with the area Ai, and the heights hi are perpendicular to the faces or to their extensions and are originated from the point O that joins the vertices of all the pyramids Semenchenko, Thus the volume of the polyhedron is V' - -3 1Z A, hi.
Hence, the second term gives the condition of equilibrium of masses Eq. So in the state of thermodynamic equilibrium a given single crystal can be confined only by the facets with their adequate Miller indices that satisfy equality 3. This is the well-known Wulff's theorem. On the basis of the above theorem Wulff proposed a geometrical method of construction of the equilibrium form of a single crystal. This construction, illustrated in Fig. Through a fixed point O in the space, we draw straight lines which map crystallographic directions [hkl] of the given lattice. Starting from the point O, a set of vectors with their lengths proportional to a hkl is drawn along the straight lines.
At the end of each vector the plane perpendicular to it is constructed. Then the inner envelope of the planes will determine the equilibrium form of the crystal Fig. The Wulff theorem is a realization of Gibbs' idea. According to the latter, the equilibrium form of a c r y s t a l - if the volume forces are not exerted - is determined by the minimum value of surface integral of the surface energy a hkl at a constant volume.
Assuming the volume of the single crystal of interest to be V0, as in 3. It follows from 3. Accordingly, if for a given crystallographic structure the fixed form of the single crystal is a regular polyhedron then, in general, the equilibrium form may be also bounded by facets which not necessarily belong to the polyhedron i.
The left side of that equation is the work L s, needed to create the entire surface of the crystal. Thus it can be seen that the Wulff constant is simply related to the total energy required for crystal formation. The envelope satisfies Wulff's law and, moreover, its shape provides additional information about the crystal in the equilibrium state: The conclusion given by Landau is as follows: Atomic microcrystals have a reasonable chance to attain the equilibrium shape. In the case of large single crystals the time needed to obtain the equilibrium form is practically infinite.
The beautiful experimental verification of the Wulff theorem was given by Heyraud and Metois These authors demonstrated that for micron sized crystalline particles equilibrated with their own vapor the shape of the particle was consistent with a Wulff construction independent of the actual size. If the orientation of the surface confining a crystal differs negligibly from that of the most stable plane, corresponding to the singularity in the a-surface a closepacked plane , then we obtain a crystal surface consisting of several terraces of oneor two-atom height which continue the orientation of the close-packed, stable plane Fig.
Since the orientation of such plane is vicinal to that of a close-packed low-index plane, such planes are called vicinal planes.
- Great Expectations;
- Souvenirs de la maison des morts (French Edition).
- Metal Surface Electron Physics - PDF Free Download.
- Work function;
- An Imported Wife (Mills & Boon Vintage 90s Modern).
- The Elemental Dance (The Elemental Tales Book 2);
- .
- Loop the Loop;
- .
- Câncer e Prevenção (Portuguese Edition).
- ;
They are characterized by high Miller indices. Terraces at the solid surface. Let a be the angle constituted by a vicinal plane with the close-packed one. Vicinal planes can be depicted as the fragments a of the surface near singularities Nagaev, This justifies the utility of the liquid-drop model in describing small crystals.
Such a high pressure causes the change in the lattice parameter at the surface of small crystals. It follows from formula 3. The increased pressure inside the crystal will lead to a contraction of the lattice parameter with the decreasing particle size. In general, the lattice parameters of metallic particles are reported to contract although in some cases no changes are observed Marks, The change in the lattice parameter with the size of the aluminum crystallite is displayed in Fig. This is a illustration of the classical size effect, that is the effect of the specimen size on a physical quantity.
The measurements of change in the lattice parameter as a function of a particle size allow to determine, in connection with Eq. Dependence of the pressure, pr, inside the microscopic crystal on its size. Redrawn Another size effect of this type namely, the lowering of the melting temperature of small crystallites, 9 was predicted by Pawlow in Pawlow, This phenomenon can be explained as follows. Let us consider a one-component system of the crystal remaining in the state of equilibrium with its saturated vapor. Differentiating this equation with respect to temperature, pressure and the hi, and taking into account the relation 3.
From the equality 3. The experimental data illustrating a lowering of the melting point of gold are given in Fig. Dependence of the melting temperature on the particle size. Redrawn with permission from Borel This is connected with a fact that for liquids the two quantities are equal.
The process of formation of a surface of solid can be divided into two stages. First, the crystal is cleaved in two parts, which results in obtaining two new surfaces. The energy required to create unit area of a new surface is the surface energy.
On cleaving the crystal the work needed to break a certain number of atomic bonds is performed. The breaking of the atomic bonds leads to the appearance of stresses near the surface, which cause the displacement of surface atoms to new positions. In order to attain that the new positions were equilibrium ones, some forces should be applied to the surface edges, that would equilibrate the action of the stresses existing within the crystal. The surface force acting on the unit length will be called a surface stress and denoted by the g.
In the case of deformation or cleavage of a liquid drop the atoms or molecules inside the liquid change their positions and a new surface is formed. As the result, both stages of surface formation in a liquid merge into the one and the work performed during such process is given by formula 3. In order to distinguish between the surface energy, or, and the surface stress, g, let us try at first to determine the relation between a and the thermodynamic quanti- 46 CHAPTER 3.
Plot of the density of the one-component system crystal-vapor versus distance. In the most common approach given by Gibbs, the phases in the bulk of crystal are regarded to be spatially homogeneous up to the interface. For a one-component system which consists of a solid remaining in equilibrium with its vapor, the distribution of density is presented in Fig.
The quantity X, which may represent e. Schematic outline of the surface phase, where the surface excess of particles equals zero. The a defined in this manner does not depend on the choice of the dividing plane. As it is seen from 3. However, since the position of the phase boundary plane i. For this reason, sometimes also a is called the surface specific free energy. In the general case of the anisotropic solid, the surface stress is strongly direction dependent.
Let us consider a flat surface of a crystal with the area A and surface energy, a. Here we have adopted the usual convention that repeated index denotes summation over this index. Positive gij means that the surface would prefer to contract within the surface plane. A more detailed derivation of equation 3.
Surface tension is a scalar measure of the surface stress thus, it is given in the units of force per unit length. In the case of an isotropic solid the stress tensor gij has only diagonal components, i. Thus the last term in 3. This implies the breaking of a certain number of bonds of every surface atom with its neighbors. This yields the correct order of magnitude of the measured surface energy. We will come back to the discussion of surface energy and of surface stress in Chap.
The great electrical conductivity of metals, as well as their high reflectivity suggest that they contain a large number of electrons which can move freely in the crystal skeleton build up from the positively charged ion-cores. This means, that the real electrostatic potential, V r , which is periodic inside the crystal, may be replaced by a constant one.
Moreover, since electrons are trapped by the metallic ions inside the metal, Sommerfeld represented this bounding by an infinite potential barrier placed at the metal surface. On the other hand the components of k-vectors defined by 4. The factor of two appearing in the nominator comes from the spin. According to the Pauli principle two one-electron states with opposite spins can be assigned to every k-point.
In the ground state at temperature T - 0 K , each of the states up to a maximum kmax is occupied by two electrons. Thus the points in the k-space fill a sphere of radius kmaz, called Fermi sphere. Consequently the maximum value kmax is called Fermi momentum or Fermi wave number and is denoted as kF. Making use of Eqs 4. A word of caution should be said here. The term Wigner-Seitz radius, as applied to r s parameter, is somewhat misleading. In fact the Wigner-Seitz radius denotes the radius of the sphericalized Wigner-Seitz cell compare Sec. The number of electrons in a metal N - ZNo. The chemical potential, ' fixed by the relation 4.
The simplest way of accounting for the presence of a surface of metallic sample is to replace the three dimensional box by a slab of finite thickness L in xdirection, and extended infinitely in the y- and z-directions. For such an infinite barrier model IBM we can replace the actual infinite set of wave functions for free electron model by a finite number, imposing the Born-vonK a r m a n boundary conditions, characterized by a period L in the y- and z-directions, and fixed boundary at x - L Bardeen, ; Sugiyama, Consequently, the appropriate wave functions will have the form 4.
Electron density profile for the infinite dashed line and finite-square-potential barrier model of metal surface. The electron density distribution profile near impenetrable infinite-barrier is illustrated in Fig. This form of oscillations is called the Friedel oscillations. In the case of a real metal, thermionic or photo-emission of electrons is observed. Thus, a model of metal in order to be realistic, must give electrons possibility to leave a metal. To allow for this the motion of the free electrons of a metal can be simulated by the motion of electrons in the finite potential well Fig.
For such a finite-square-potential barrier, the SchrSdinger equation can be separated into two sets of three equations for each of the regions D1 and D2: Energy diagram for the metal-surface problem. We have also assumed that potential energy of an electron at infinity is equal zero. In this model the positive charge of point ions is smeared out uniformly over the volume of the crystal forming a sort of metallic jelly.
This may be seen from the following simple consideration. The above argumement suggests that jellium model may be accepted as a rather good approximation for surface problems of large metallic samples, but its applicability to the fine particles must be considered with care. It originates from two words: Positive charge distribution for the uniform background model jellium. Metal as a whole must remain neutral. It means that the total charge negative and positive integrated over the whole space must be equal zero.
In the case of the semi-infinite metal represented by jellium, with the x-axis oriented perpendicular to the surface, the Eq. Illustration of the position, a, of the physical surface for the finite-square-potential barrier. For the wave functions 4. To fix the position, a Fig. The shift of the jellium edge for the finite and infinite potential barrier is illustrated in Fig. It follows from Eqs 4. We see, therefore, that the application of jellium model and the regard of the charge neutrality condition leads to the solution of the problem stated above: This can be obtained by employment of the adiabatic or Born-Oppenheimer approximation.
The adiabatic approximate Schr5dinger equation, for the electrons in a static lattice of ions, can be written in the form: The last term on the lhs of Eq. It is posssible, however, to transform this many-electron problem of Eq. Then the potential seen by the electron at ri will be: The Pauli exclusion principle, generalized to the many-body case, demands from the wave function 4.
The wave function of the form 4. The second term in 4. The third, exchange term in 4. We shall make use of Eq. Using these functions, for a metal represented by jellium model one can easily calculate the exchange energy Raimes, to get k 4. Especially, a more detailed consideration of their electrostatic repulsion is needed, which accounts for the reduced probability of close encounters of electrons, particularly those of antiparallel spin. The difference between the exact energy of the ground state and the Hartree-Fock energy, E H F , is called correlation energy, Ec - E e x a c t - This energy accounts for the correlated to their Coulomb repulsion.
The Wigner expression for the simple form 0. The exchange Fermi hole in the electron distribution of bulk metal. Thus, one may conclude that each of free electrons in the bulk jellium is surrounded by the so called Fermi hole, of approximate radius r s, in the distribution of electrons with parallel spins.
Formats and Editions of Metal surface electron physics [theranchhands.com]
The spherical shape of the Fermi hole will be modified in the vicinity of the surface Fig. In order to answer the question, how the average Fermi hole will be changed near the metal surface, one may calculate nx r12 using the wave functions 4. From the schematic picture of Fig. The results of calculations have shown Juretschke, that as the electron approaches the surface its exchange hole flattens and remains behind, in the region of high-charge density.
When electron is far away from a metal surface, the exchange hole is flattening out to a thin planar charge deficit excluding in total a charge of - l el from the electron distribution. This hole together with its counterpart for the electrons with antiparallel spin, the correlation hole, gives an image charge distribution. As we will see a microscopic picture of the image force, which arises when electron is brought out of a metal, is determined by the electron exchange and correlation effects see Chapter Schematic illustration of the exchange hole for an electron dot near the metal surface.
The vertical dashed line shows the image plane position. The lower part shows the electron density profiles. Redrawn with permission from Serena et al. The total energy of this system will consist of the electrostatic, kinetic and exchange-correlation contributions. Let us consider each of the contributions to the total energy inside a single Wigner-Seitz cell. The electrostatic Coulomb energy of a charged sphere will consist of three contributions: To calculate the electrostatic self-energy of the uniform electron gas we determine first the electrostatic potential V r of the uniformly charged sphere Fig.
Calculation of the potential of the uniformly charged sphere. On the other hand these two positive contributions are compensated by the negative energy of electrons interaction with the uniform positive background. The energy per particle in jellium given by 4. It means that jellium is stable only at the equilibrium 0.
Energy per electron in jellium versus density parameter rs. The bulk energy term, proportional to the volume, can be determined for a large sample in which the distribution of electrons is uniform throughout. The surface energy term, proportional to the surface area, is determined in turn by the non-uniform distribution of electrons gas near the surface of the metal. This nonuniformity gives the total energy which is in excess of what would be expected if the uniform electron density was terminated abruptly at the surface.
This excess is the surface energy of the electron gas. We can define surface energy, a, as the work per unit area required to split the crystal in two fragments along a plane. Let E be the energy of the electrons in the unsplit specimen and Es the energy of electrons in each half of the split one. For instance, in the Sommerfeld model of metal the surface kinetic energy is few times larger than the electrostatic energy contribution originating from the creation of surface double layer. As an instructive example we will sketch within this model, the calculation of the contribution to the surface energy arising from the sum of one-electron energies.
It is useful to impose the periodic boundary conditions in yand z-directions and the standing wave in the x-direction. Splitting of the macroscopic block of a metal. The total energy, E, of the uncut block is equal to the sum over occupied states h2 k. Below is a table of work function values for various elements. Note that the work function depends on the configurations of atoms at the surface of the material.
For example, on polycrystalline silver the work function is 4. Due to the complications described in the modelling section below, it is difficult to theoretically predict the work function with accuracy. Various trends have, however, been identified. The work function tends to be smaller for metals with an open lattice, and larger for metals in which the atoms are closely packed. It is somewhat higher on dense crystal faces than open crystal faces, also depending on surface reconstructions for the given crystal face.
The work function is not simply dependent on the "internal vacuum level" inside the material i. A variety of factors are responsible for the surface electric dipole. Even with a completely clean surface, the electrons can spread slightly into the vacuum, leaving behind a slightly positively charged layer of material.
This primarily occurs in metals, where the bound electrons do not encounter a hard wall potential at the surface but rather a gradual ramping potential due to image charge attraction. The amount of surface dipole depends on the detailed layout of the atoms at the surface of the material, leading to the variation in work function for different crystal faces. In a semiconductor , the work function is sensitive to the doping level at the surface of the semiconductor.
Since the doping near the surface can also be controlled by electric fields , the work function of a semiconductor is also sensitive to the electric field in the vacuum. The reason for the dependence is that, typically, the vacuum level and the conduction band edge retain a fixed spacing independent of doping. This spacing is called the electron affinity note that this has a different meaning than the electron affinity of chemistry ; in silicon for example the electron affinity is 4.
From this one might expect that by doping the bulk of the semiconductor, the work function can be tuned. In reality, however, the energies of the bands near the surface are often pinned to the Fermi level, due to the influence of surface states. Theoretical modeling of the work function is difficult, as an accurate model requires a careful treatment of both electronic many body effects and surface chemistry ; both of these topics are already complex in their own right. One of the earliest successful models for metal work function trends was the jellium model, [17] which allowed for oscillations in electronic density nearby the abrupt surface these are similar to Friedel oscillations as well as the tail of electron density extending outside the surface.
This model showed why the density of conduction electrons as represented by the Wigner-Seitz radius r s is an important parameter in determining work function. The jellium model is only a partial explanation, as its predictions still show significant deviation from real work functions. More recent models have focussed on including more accurate forms of electron exchange and correlation effects, as well as including the crystal face dependence this requires the inclusion of the actual atomic lattice, something that is neglected in the jellium model.
The electron behavior in metals varies with temperature and is largely reflected by the electron work function. A recent theoretical model for predicting the temperature dependence of the electron work function, developed by Reza Rahemi et. From Wikipedia, the free encyclopedia. Volta potential and Kelvin probe force microscope. It treats the work function changes due to alkali metal adsorption on metals, adhesion between metals and discusses the universal aspects of the binding energy curves.
In each case extensive reference lists are provided. During the last thirty years metal surface physics, or generally surface science, has come a long way due to the development of vacuum technology and the new surface sensitive probes on the experimental side and new methods and powerful computational techniques on the theoretical side. The aim of this book is to introduce the reader to the essential theoretical aspects of the atomic and electronic structure of metal surfaces and interfaces. The book gives some theoretical background to students of experimental and theoretical physics to allow further exploration into research in metal surface physics.
Work function of simple metals: Variational electron density profiles: Dieses eBook kann mit fast allen eBook-Readern gelesen werden. Mit dem amazon-Kindle ist es aber nicht kompatibel.
