Werner Heisenberg in photo: This quantum fuzziness lies behind one of the most famous principles of quantum physics: In the German physicist, Werner Heisenberg , framed the principle in terms of measuring the position and momentum of a quantum particle, say of an electron. The momentum of an object is its mass times its velocity. The uncertainty principle states that you cannot know, with absolute certainty, both the position and momentum of an electron — the more accurately you measure one of these properties the less accurate your knowledge of the other.
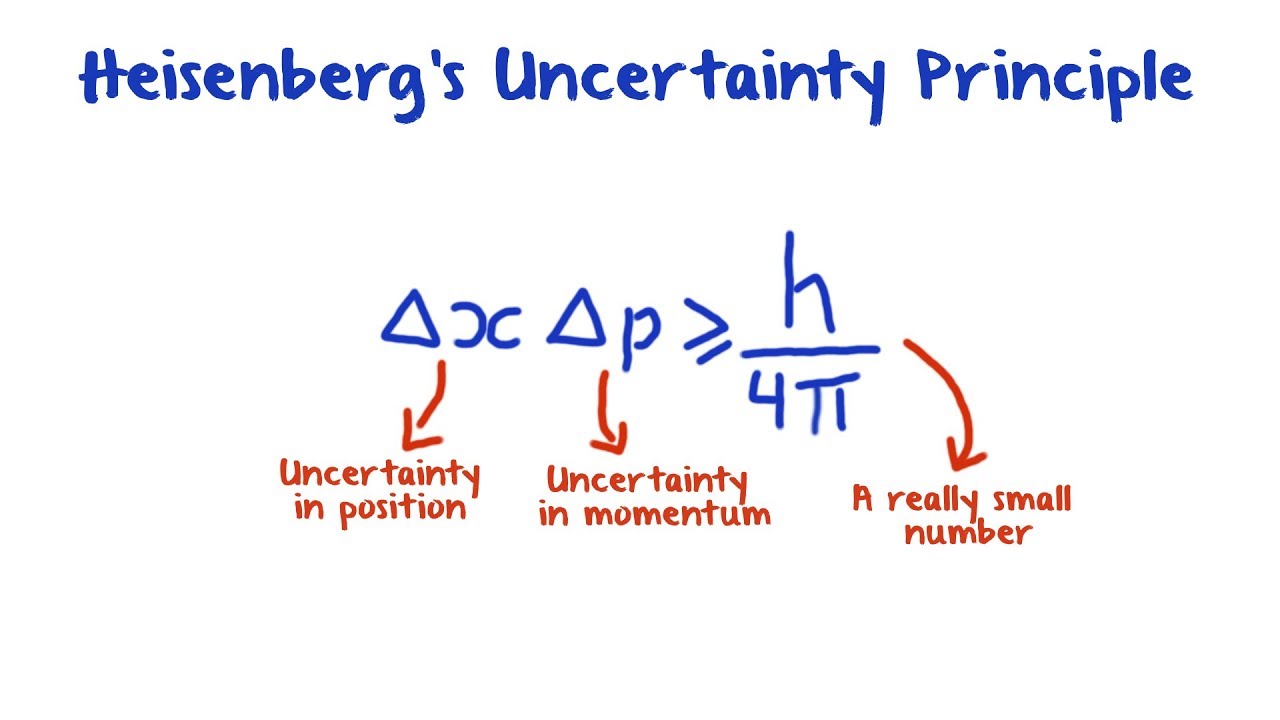
If we write the uncertainty in a particle's position as , and the uncertainty in a particle's momentum as , then the uncertainty of these two properties is connected in the following way: This is the most common mathematical expression of Heisenberg's uncertainty principle, that the product of these uncertainties has a minimum value. But the principle extends to other pairs of particles called complementary variables , such as length of time and energy, whose connection is expressed in similar inequalities.
Heisenberg himself tried to understand this principle physically using the following thought experiment. Suppose you wanted to locate the position of an electron. To do this you would use a microscope which bounces photons of light of an object in order to observe it. The accuracy of a microscope is limited by the wavelength of the light used — the shorter the wavelength the more accurate your observations.
Heisenberg suggested using a gamma-ray microscope as gamma-rays are a type of light with a very short wavelength. But the tradeoff is that light waves with a shorter wavelength have a higher frequency, and the photons have correspondingly higher energy. This is because for waves, where is the speed of the wave, is the wavelength and is the frequency. The speed of light is fixed at so as the wavelength decreases the frequency must increase. And the energy, , of a photon is given by. But Planck's constant , appearing in the uncertainty principle, determines the size of the confinement that can be produced by these forces.
Another way of saying it is that the strengths of the nuclear and electromagnetic forces along with the constraint embodied in the value of Planck's constant determine the scales of the atom and the nucleus. The following very approximate calculation serves to give an order of magnitude for the energies required to contain particles. The other reason for doing it was to get an electron confinement energy close to what is observed in nature for comparison with the energy for confining an electron in the nucleus.
What is Heisenberg's Uncertainty Principle? | Science | The Guardian
This is because this approach only confines the electron in one dimension, leaving it unconfined in the other directions. For a more realistic atom you would need to confine it in the other directions as well. A better approximation can be obtained from the three-dimensional particle-in-a-box approach, but to precisely calculate the confinement energy requires the Shrodinger equation see hydrogen atom calculation. The Uncertainty Principle The position and momentum of a particle cannot be simultaneously measured with arbitrarily high precision. Similarly, a wave with a perfectly measurable momentum has a wavelength that oscillates over all space infinitely and therefore has an indefinite position.
You could do the same thought experiment with energy and time. To precisely measure a wave's energy would take an infinite amount of time while measuring a wave's exact instance in space would require to be collapsed onto a single moment which would have indefinite energy.
Keep Exploring Britannica
The Heisenberg Principle has large bearing on practiced science and how experiments are designed. To create a measurement, an interaction with the particle must occur that will alter it's other variables. For example, in order to measure the position of an electron there must be a collision between the electron and another particle such as a photon. This will impart some of the second particle's momentum onto the electron being measured and thereby altering it.
A more accurate measurement of the electron's position would require a particle with a smaller wavelength, and therefore be more energetic, but then this would alter the momentum even more during collision. An experiment designed to determine momentum would have a similar effect on position.
Heisenberg uncertainty principle
Consequently, experiments can only gather information about a single variable at a time with any amount of accuracy. The volume is not the property that matters, but the mass.
- Uncertainty principle.
- I Carry the Cross, too: The Completion of the Message of Jesus Christ;
- Heisenberg's Uncertainty Principle - Chemistry LibreTexts.
So convert to mass with density. One example that can be used is a glass of water in a cup holder inside a moving car. This glass of water has multiple water molecules each consisting of electrons.
- Operational Weather Forecasting (Advancing Weather and Climate Science).
- Heisenberg's uncertainty principle?
- What is Heisenberg's Uncertainty Principle?!
- Secondary menu.
- Historical Dictionary of German Theater (Historical Dictionaries of Literature and the Arts)?
- Alien?.
The water in the glass is a macroscopic object and can be viewed with the naked eye. The electrons however occupy the same space as the water, but cannot be seen and therefore must be measured microscopically. Thus, the uncertainty principle has much greater bearing on the electrons rather than the macroscopic water.
