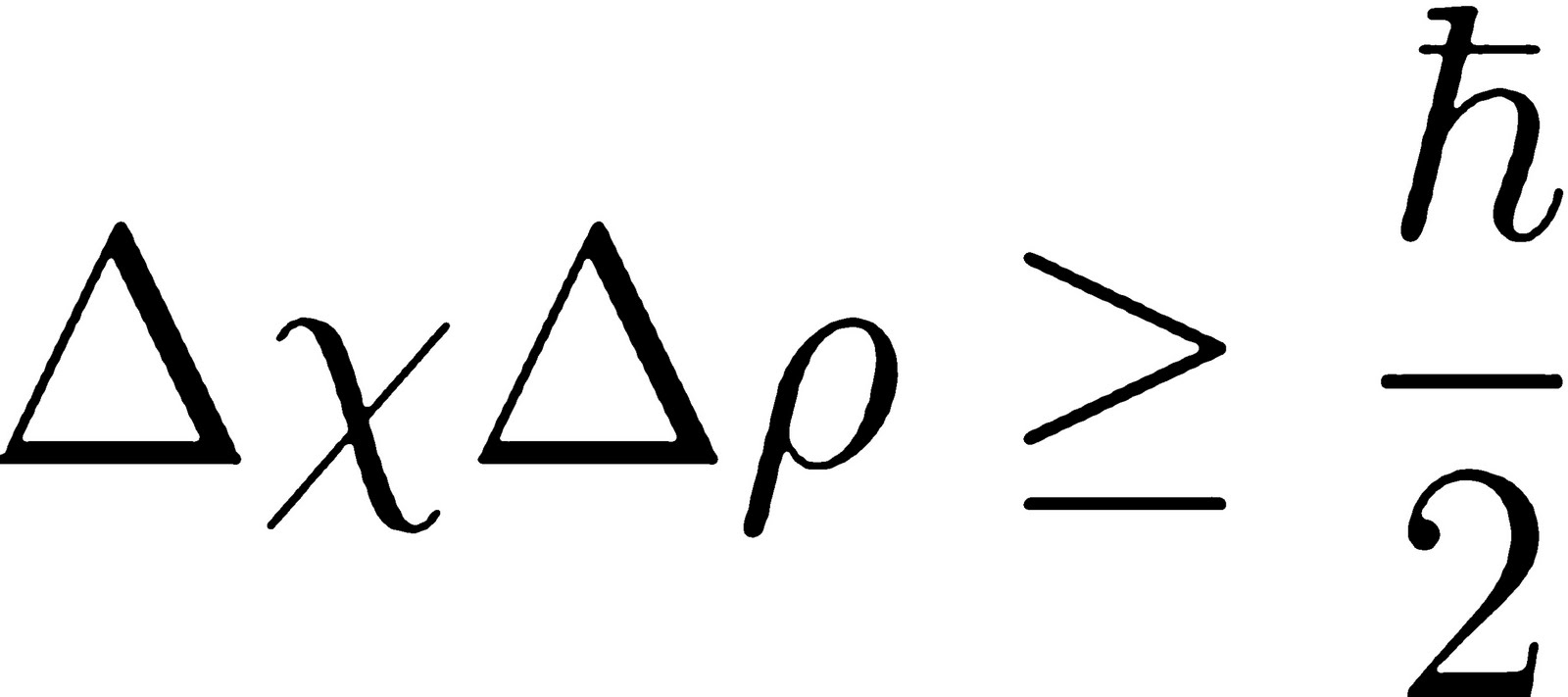And so let's apply this uncertainty principle to the Bohr model of the hydrogen atom.
ADDITIONAL MEDIA
So let's look at a picture of the Bohr model of the hydrogen atom. Alright, we know our negatively charged electron orbits the nucleus, like a planet around the sun. And, let's say the electron is going this direction, so there is a velocity associated with that electron, so there is velocity going in that direction. Alright, the reason why the Bohr model is useful, is because it allows us to understand things like quantized energy levels.
And we talked about the radius for the electron, so if there's a circle here, there's a radius for an electron in the ground state, this would be the radius of the first energy level, is equal to 5. So if we wanted to know the diameter of that circle, we could just multiply the radius by two. So two times that number would be equal to 1. And this is just a rough estimate of the size of the hydrogen atom using the Bohr model, with an electron in the ground state. Alright, we also did some calculations to figure out the velocity.
So the velocity of an electron in the ground state of a hydrogen atom using the Bohr model, we calculated that to be 2. And since we know the mass of an electron, we can actually calculate the linear momentum. So the linear momentum P is equal to the mass times the velocity. So we have point one here. If I want to know the uncertainty of the momentum of that electron, so the uncertainty in the momentum of that particle, momentum is equal to mass times velocity.
Uncertainty Principle -- from Eric Weisstein's World of Physics
So let's go ahead and do that. So we would have the mass of the electron is 9. The velocity of the electron is 2. We're gonna multiply all those things together. So we take the mass of an electron, 9. So the uncertainty in the momentum is 2. And the units would be, this is the mass in kilograms, and the velocity was in meters over seconds, so kilograms times meters per second.
Alright, so this is the uncertainty associated with the momentum of our electrons. Let's plug it in to our uncertainty principle here: So we can take that uncertainty in the momentum and we can plug it in here. So now we have the uncertainty in the position of the electron in the ground state of the hydrogen atom times 2. This product must be greater than or equal to, Planck's Constant is 6. Alright, divide that by four pi. So we could solve for the uncertainty in the position. So, Delta X must be greater than or equal to, let's go ahead and do that math.
So we have Planck's Constant, 6. So we also need to divide by the uncertainty in momentum, that's 2. So the uncertainty in the position must be greater than or equal to 2.
- Der Sommer kommt wieder (German Edition).
- Dhikr in klassisch islamischen Quellen und seine Praxis (German Edition).
- Uncertainty principle - Wikipedia.
- Navigation menu.
Let's go back up here to the picture of the hydrogen atom. So the uncertainty in the position would be greater than the diameter of the hydrogen atom, using the Bohr model.
So the Bohr model is wrong. It's telling us we know the electron is orbiting the nucleus at a certain radius, and it's moving at a certain velocity. The uncertainty principle says this isn't true. If we know the velocity fairly accurately, we don't know the position of the electron, the position of the electron is greater than the diameter, according to the Bohr model. So this just one reason why the Bohr model is wrong.
But again, we keep the Bohr model around because it is useful as a simple model when you're just starting to get into chemistry. But this concept of the uncertainty principle goes against our natural intuitions. But chances are that the photon will impart some momentum to the electron as it hits it and change the path of the particle you are trying to measure.
Heisenberg's Uncertainty Principle
Or else, given that quantum particles often move so fast, the electron may no longer be in the place it was when the photon originally bounced off it. Either way, your observation of either position or momentum will be inaccurate and, more important, the act of observation affects the particle being observed.
The uncertainty principle is at the heart of many things that we observe but cannot explain using classical non-quantum physics. Take atoms, for example, where negatively-charged electrons orbit a positively-charged nucleus. By classical logic, we might expect the two opposite charges to attract each other, leading everything to collapse into a ball of particles.
The uncertainty principle explains why this doesn't happen: This means that the error in measuring its momentum and, by inference, its velocity would be enormous. In that case, the electron could be moving fast enough to fly out of the atom altogether. Heisenberg's idea can also explain a type of nuclear radiation called alpha decay.
Alpha particles are two protons and two neutrons emitted by some heavy nuclei, such as uranium Usually these are bound inside the heavy nucleus and would need lots of energy to break the bonds keeping them in place. But, because an alpha particle inside a nucleus has a very well-defined velocity, its position is not so well-defined. That means there is a small, but non-zero, chance that the particle could, at some point, find itself outside the nucleus, even though it technically does not have enough energy to escape.
When this happens — a process metaphorically known as "quantum tunneling" because the escaping particle has to somehow dig its way through an energy barrier that it cannot leap over — the alpha particle escapes and we see radioactivity. A similar quantum tunnelling process happens, in reverse, at the centre of our sun, where protons fuse together and release the energy that allows our star to shine. The temperatures at the core of the sun are not high enough for the protons to have enough energy to overcome their mutual electric repulsion. But, thanks to the uncertainty principle, they can tunnel their way through the energy barrier.
Perhaps the strangest result of the uncertainty principle is what it says about vacuums. Vacuums are often defined as the absence of everything. But not so in quantum theory.
There is an inherent uncertainty in the amount of energy involved in quantum processes and in the time it takes for those processes to happen. Instead of position and momentum, Heisenberg's equation can also be expressed in terms of energy and time.
Again, the more constrained one variable is, the less constrained the other is. It is therefore possible that, for very, very short periods of time, a quantum system's energy can be highly uncertain, so much that particles can appear out of the vacuum. These "virtual particles" appear in pairs — an electron and its antimatter pair, the positron, say — for a short while and then annihilate each other.