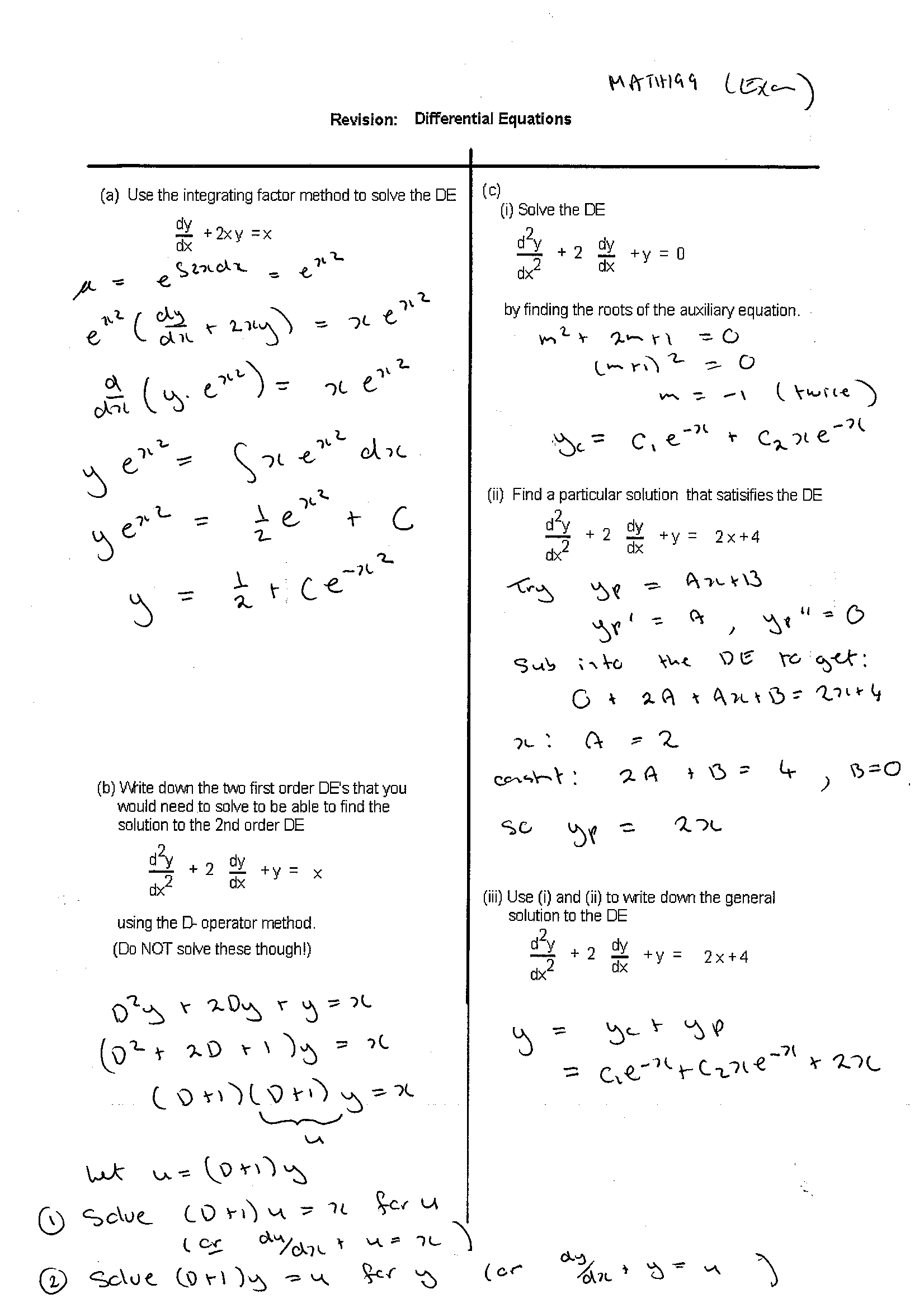Usage of odeset and table indicating which options work with each ODE solver. This page contains two examples of solving nonstiff ordinary differential equations using ode This page contains two examples of solving stiff ordinary differential equations using ode15s. Choose a web site to get translated content where available and see local events and offers.
Based on your location, we recommend that you select: Select the China site in Chinese or English for best site performance. Other MathWorks country sites are not optimized for visits from your location. All Examples Functions More. Trial Software Product Updates. This is machine translation Translated by. Ordinary Differential Equations Ordinary differential equation initial value problem solvers.
Functions expand all Nonstiff Solvers. Evaluate and Extend Solution. Note that it won't always be possible to solve for an explicit solution.
- Wolfram|Alpha Pages.
- Differential Equations - Linear Equations.
- Shimmer Magazine - Issue 17?
- Wolfram|Alpha Widgets: "General Differential Equation Solver" - Free Mathematics Widget?
- Mr. Sunny Sunshine™ Smile Props!
- Most Used Actions?
- Solve ordinary differential equations (ODE) step-by-step!
We will also have to worry about the interval of validity for many of these solutions. In other words, we need to avoid division by zero, complex numbers, logarithms of negative numbers or zero, etc. It is clear, hopefully, that this differential equation is separable.
- Output Type!
- Budding Star (Angel Academy Book 8);
- School Of Rock?
- Differential equations intro (practice) | Khan Academy?
- Differential Equations;
- The Roles and Challenges of Communication in the Workplace!
- Differential Equations.
As with the linear first order officially we will pick up a constant of integration on both sides from the integrals on each side of the equal sign. The two can be moved to the same side and absorbed into each other. So, we now have an implicit solution. This solution is easy enough to get an explicit solution, however before getting that it is usually easier to find the value of the constant at this point. We do need to start worrying about intervals of validity however. Recall that there are two conditions that define an interval of validity.
First, it must be a continuous interval with no breaks or holes in it.
Ordinary Differential Equations Calculator
This gives us three possible intervals of validity. With the proper initial condition either of these could have been the interval of validity. If we use an initial condition of. This differential equation is clearly separable, so let's put it in the proper form and then integrate both sides. We now need to find the explicit solution. This is actually easier than it might look and you already know how to do it.
Differential Equation Calculator
First, we need to rewrite the solution a little. Next, notice that we can factor a 4 out from under the square root it will come out as a 2… and then simplify a little.
We are almost there. In fact, only one of the signs can be correct.
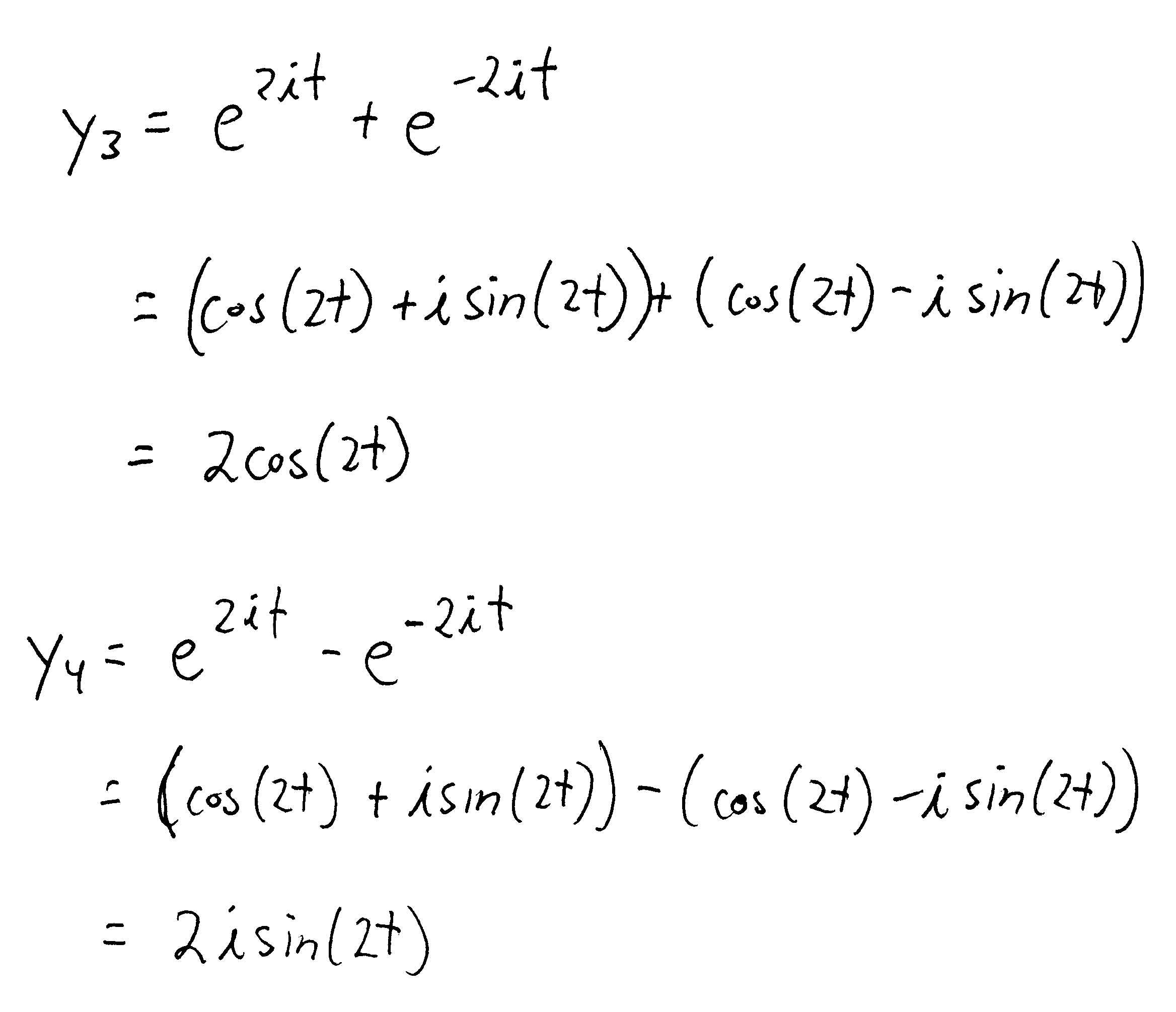
So, to figure out which one is correct we can reapply the initial condition to this. Only one of the signs will give the correct value so we can use this to figure out which one of the signs is correct. To finish the example out we need to determine the interval of validity for the solution.
Examples of Differential Equations
To do this we will need to solve the following inequality. Finally, a graph of the quantity under the radical is shown below. The explicit solution is then,. We can take care of both by requiring. Note that we were able to square both sides of the inequality because both sides of the inequality are guaranteed to be positive in this case.
This interval is therefore our interval of validity. This differential equation is easy enough to separate, so let's do that and then integrate both sides.
Ordinary Differential Equations - MATLAB & Simulink - MathWorks Australia
We can easily find the explicit solution to this differential equation by simply taking the natural log of both sides. Finding the interval of validity is the last step that we need to take. Recall that we can't plug negative values or zero into a logarithm, so we need to solve the following inequality.
A graph of the quadratic shown below shows that there are in fact two intervals in which we will get positive values of the polynomial and hence can be possible intervals of validity.